Sudoku er morsomt, motiverende og fenger selv «svake» elever. men ikke veldig rettet mot kompetansemålene. De samme mekanismene kan utnyttes for innlæring av algebra. En sentral teknikk i R1 er å faktorisere andregradsuttrykk. Den robuste metoden finner nullpunktene til andregradsuttrykket ved andregradsformelen, noe som krever litt pugg og en del utregninger. Men svært mange R1-oppgaver har uttrykk med lave heltallskoeffisienter. Som \(x^2-x-6\). De kan faktoriseres med et enklere «knep».
Anta at det er produktet av to førstegradsuttrykk \((x+a)\) og \((x+b)\). Multiplisert sammen blir det \(x^2+(a+b)x+a\cdot b\). Å faktorisere blir da det samme som å finne to tall som er slik at summen blir -1 og produktet blir 6. Produktet er enklest å ta utgangspunkt i dersom koeffisientene er hele tall, det er bare \(1\cdot 6\) og \(2 \cdot 3\) som gir 6. Siden konstantleddet er negativt, må en av faktorene være negativ. Summen av 1 og 6 kan ikke bli 1 uansett hvilket ledd som er negativt, men \(2-3=-1\) Dermed er\[x^2-x-6 = (x+2)(x-3)\]
Figurer
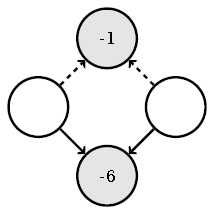
Dersom andregrads-koeffisienten ikke er 1, blir det litt mer komplisert, men Jason Dyer foreslo å lage det som en pusleoppgave. Dersom stiplede linjer peker til en sirkel, skal tallet i den være summen av sirklene som peker på den. Dersom linjene er heltrukne, skal tallet være produktet av de som peker på.

Begrensninger
Dette er kun effektivt dersom koeffisientene er heltall eller veldig enkle brøker. Andregradsformelen må være tilgjengelig som reservemetode dersom det skal regnes med desimaltall i fysikk eller kjemi. Det er ikke like lett å gi svar med kvadratrøtter eller avgjøre om uttrykket har reelle nullpunkt.
Oppgaveark
Jason Dyer har tre oppgaveark han har laget, som bygger opp mot andregradsfiguren. For å overdrive litt har han en slik figur som faktoriserer tredjegradsuttrykk, den er i beste fall kuriøs.
I tillegg har jeg laget et som er tilpasset Aschehougs læreverk. Dette kunne sikkert også ha vært laget digitalt og interaktivt, men det fungerer veldig greit med blyant og ark.