I mange algoritmer, gjentar du den samme operasjonen med nye argumenter til målet er oppnådd. I stedet for å lage en for- eller while-løkke kan en del slike algoritmer enkelt bli beskrevet med rekursjon, hvor neste steg er avhengig av tidligere steg. Denne typen algoritmisk tenkning er litt anderledes enn med løkker, men python lar funksjoner kalle seg selv og det kan i noen tilfeller gi en mer intuitiv løsning.
Forutsetninger for rekursjon
For å formulere problemet med rekursjon slik, må du ha klart:
- Et grunntilfelle, en situasjon hvor resultatet er klart definert. For trekanttallene at T1 = 1.
- Et nytt argument til neste funksjonskall, for trekanttallene blir det: en mindre enn tallet du er på.
- At problemet kommer nærmere grunntilfellet, som regel blir problemet mindre og mindre.
Summen av en liste
Et veldig enkelt eksempel kan være å legge sammen alle tallene i en liste. En måte å beskrive en algoritme for det, er at summen av listen er verdien av det første leddet pluss summen av resten av listen. Hvis det ikke er noen rest, skal du bare legge til det første leddet.
def sum_rekursiv(liste):
if len(liste) == 1:
return liste[0]
else:
return liste[0] + sum_rekursiv(liste[1:])print(sum_rekursiv([2,5,3,9,5])) gir 24.
2 + sum_rekursiv([5,3,9,5])) blir til 2 + 5 + sum_rekursiv([3,9,5])) og så videre, ned til 2 + 5 + 3 + 9 + 5.
Summen av en liste, med «splitt og hersk»
Ofte kan problemet deles opp i flere like delproblemer, som enkelt kan løses for seg. Summen av en liste kan også uttrykkes som summen av den første halvdelen av listen, lagt sammen med summen av den andre halvdelen av listen.
def sum_rek(liste):
if len(liste) == 1:
return liste[0]
else:
midt = len(liste) // 2 # Heltallsdivisjon
return sum_rek(liste[:midt]) + sum_rek(liste[midt:])Det doble deletegnet gir deg heltallsdelen av kvotienten, 25 // 4 blir 6 fordi 25 kan skrives som 4 * 6 +1. Med funksjonen over blir sum_rek([2, 5,3,9,5])) til sum_rek([2, 5])) + sum_rek([3,9,5]))sum_rek([2])) + sum_rek([5])) + sum_rek([3])) + sum_rek([9,5]))2 + 5 + 3 + sum_rek([9]) + sum_rek([5]))2 + 5 + 3 + 9 + 5
Dette er et veldig enkelt eksempel, men for større og mer kompliserte problemer kan hver del bli sendt til ulike prosessorer eller datamaskiner for å bli løst samtidig.
Utvidelser
- Lag en rekursiv funksjon som returnerer argumentet sitt baklengs: «rekursiv» blir til «visruker»
- Lag en rekursiv funksjon som avgjør om en tekststreng eller liste er et palindrom, at det er likt i begge retninger. Som «regninger» eller [3, 8, 8, 3].
Nullpunkt ved halveringsmetoden og rekursjon
En måte å finne nullpunkt på, kan være å starte med en verdi hvor funksjonen er positiv, og en hvor den er negativ. Da må det være (minst) et nullpunkt i det intervallet, om funksjonen er kontinuerlig. Fortegnene først og midt i intervallet avgjør på hvilken side nullpunktet ligger. Om fortegnene er like, ligger nullpunktet i den andre halvdelen. Så gjentas algoritmen med et nytt intervall hvor midtpunktet enten blir største eller minste verdi. For å raskt sjekke om to tall har samme fortegn, kan du se på produktet av de. Produktet blir bare negativt om fortegnene er motsatte.
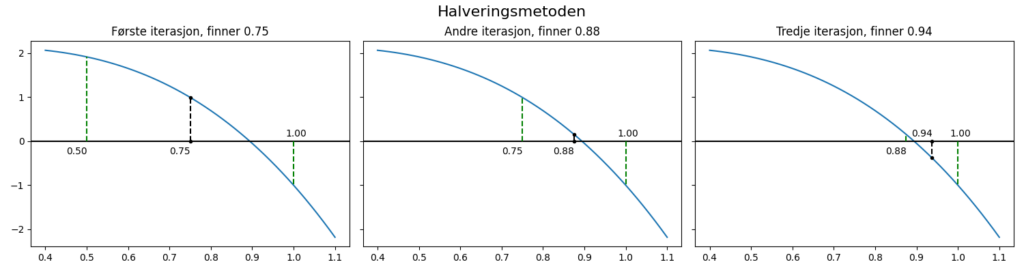
Det trengs også et kriterium for når algoritmen er ferdig. I eksempelet under kjører den et fast antall ganger. Dersom funksjonen blir kallet uten et fjerde argument, settes n til 10. Så trekkes det fra 1 for hvert nivå av rekursjon og hvis n er 0, returnerer funksjonen bare midtpunktet. Dermed stopper den etter ti funksjonskall. Legg merke til at i det tredje funksjonskallet er forslaget til nullpunkt lengre unna den faktiske verdien enn det var i det andre funksjonskallet. Men intervallet som nullpunktet må ligge i har blitt mindre, og ved å øke antallet funksjonskall kan presisjonen bli så god du vil.
def f(x):
# En funksjon hvor nullpunktet ikke kan finnes eksakt
return 2**x -4*x**3 + 1
def halvering_rekursiv(f, nedre, øvre, n=10):
midt = (øvre+nedre)/2
if n == 0:
return midt
if f(øvre)*f(midt) < 0: # Sammenligner fortegnene
return halvering_rekursiv(f, midt, øvre, n-1)
else:
return halvering_rekursiv(f, nedre, midt, n-1)Utvidelser
- Kan du få algoritmen til å stoppe når du er en gitt verdi fra 0?
- Dersom algoritmen ikke finner noe nullpunkt, kan funksjonen gi en feilmelding?
- Hva skjer dersom det er flere nullpunkt i intervallet? Kan du finne alle?
Nullpunkt ved Newtons metode
En type funksjon det er enkelt å finne nullpunkt til, er lineære funksjoner. Alle kontinuerlige funksjoner ligner på rette linjer, hvis du ser på et lite nok intervall eller «zoomer langt nok inn». En grei tilnærming er da tangenten til funksjonen i et punkt. Om du har en kandidat som nullpunkt, lager du tangenten til funksjonen for den x-verdien og finner nullpunktet til tangenten. Så gjentar du den samme prosessen med tangenten for den nye verdien.
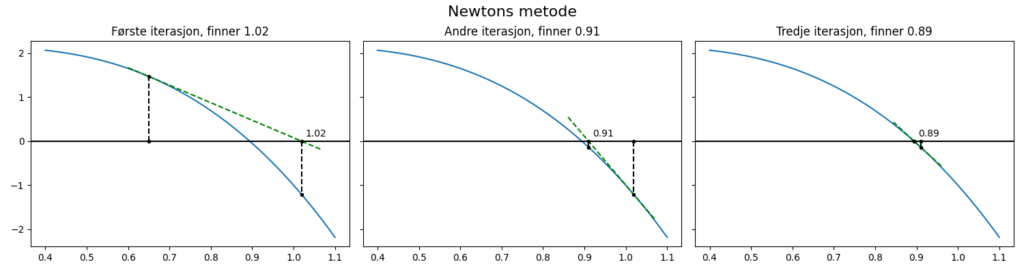
For å finne nullpunktet til tangenten, må du snu litt på ettpunktsformelen. \(y\) skal være 0, og du løser for \(x\):
\(\begin{align*}y-f(x_1) &= f'(x_1) \cdot (x-x_1)\\
\frac{-f(x_1)}{f'(x_1)} &= x-x_1\\
x &= x_1 – \frac{f(x_1)}{f'(x_1)} \end{align*} \)
Denne nye x vil, i de fleste tilfeller, være nærmere det faktiske nullpunktet.
def f(x):
# En funksjon hvor nullpunktet ikke kan finnes eksakt
return 2**x -4*x**3 + 1
def derivert(f, x, h=1e-9):
return (f(x+h)-f(x-h))/(2*h)
def newton_rekursiv(f, x, n=10):
if n == 0:
return x
else:
ny_x = x - f(x) / derivert(f, x)
return newton_rekursiv(f, ny_x, n-1)Utvidelser
- Se på de samme som for halveringsmetoden
- Hva skjer om du ser på funksjoner som \(f_1 = \sqrt[3]{x}\) og \(f_2 = x^2+1\)?
- Sammenlign hvor mye nærmere den eksakte verdien de to metodene kommer per funksjonskall.