En tallfølge kan bli beskrevet ut fra tidligere verdier og en endring. For eksempel kan vi definere trekanttallene Tn som T1 = 1, og Tn+1 = Tn + (n+1). Eller Tn = Tn-1 + n.
| n | 1 | 2 | 3 | 4 | 5 |
| Trekanttall | 1 | 3 | 6 | 10 | 15 |
| Differanse | 2 | 3 | 4 | 5 |
En direkte beregning av det femte trekanttallet i python kan være som under.
T = 0
for n in range(5):
T += n+1
print(T)Variabelen T holder på verdien av trekanttallene mens løkken teller opp.
Dersom du i python har definert en funksjon som beregner trekanttall nummer n, kan du kalle funksjonen inne i seg selv, rekursivt.
def trekanttall(n):
if n == 1:
return 1
else:
return n + trekanttall(n-1)
print(trekanttall(5))Når denne funksjonen i nederste linje kalles med argumentet 5, returnerer den 5+trekanttall(4). trekanttall(4) vil returnere 4+trekanttall(3). Slik fortsetter det ned til n er 1, og funksjonen bare returnerer 1. Resultatet blir 5 + 4 + 3 + 2 + 1 = 15.
Forutsetninger for rekursjon
For å formulere problemet med rekursjon slik, må du ha klart
- Et grunntilfelle, en situasjon hvor resultatet er klart definert. For trekanttallene at T1 = 1.
- Et nytt argument til neste funksjonskall, for trekanttallene blir det: en mindre enn tallet du er på.
- At problemet kommer nærmere grunntilfellet, som regel blir problemet mindre og mindre.
Fibonacci-tall
En vanlig tallfølge med rekursiv definisjon er Fibonacci-tallene: F1 = 1, F2 = 1, Fn = Fn-1+ Fn-2. En rekursiv funksjon i python kan være:
def fibonacci(n):
if n == 1 or n == 2:
return 1
else:
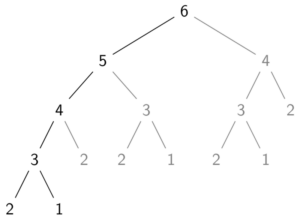
return fibonacci(n-1) + fibonacci(n-2)Denne returnerer verdiene raskt for små n, men om jeg ber om fibonacci(50), starter viften på laptopen min raskt og den bruker 25 minutter på å returnere 12586269025. Problemet er at hver gang for eksempel fibonacci-tall nummer 6 skal beregnes, må den beregne nummer 5, 4, 3, 2 og 1. For å beregne nummer 5, må den beregne 4, 3, 2 og 1. Det må den gjenta mange ganger, siden funksjonen ikke kan huske tidligere beregnede verdier.
Mer effektive teknikker
I videregående skole, hvor problemene er veldig små, er det ikke spesielt viktig hvor effektive algoritmene er. Men for større datasett og beregninger, kan det bli forskjellen på å bli ferdig raskt eller aldri.
Lagre mellomregninger
minne = {} # En litt annen type "liste", dictionary
minne[1] = 1
minne[2] = 1
def fib_rekursiv(n):
if n not in minne:
minne[n] = fib_rekursiv(n-1) + fib_rekursiv(n-2)
return minne[n]Her blir nye fibonacci-tall lagt til i en ordbok, «dictionary», som er veldig rask å slå opp i. Selve beregningen går bare en gang per tall, og øker hastigheten veldig. Denne funksjonen beregner fibonacci(50) på 0,6 sekunder, og møter ikke begrensninger før nummer 986, når feilmeldingen blir RecursionError: maximum recursion depth exceeded. Da er det for mange funksjoner «pakket inn i hverandre». F985 har 206 siffer, og burde være stort nok til det meste.
Iterativ, direkte beregning
Det er ikke alltid rekursjon er den mest effektive løsningsmetoden. For å beregne enda høyere fibonacci-tall, er det enkleste en direkte beregning som ikke tar vare på mellomverdiene.
N = 20 # Hvilket Fibonacci-tall du vil ha
a = 1
b = 1
for i in range(2,N): # De to første er allerede beregnet.
t = b # Midlertidig variabel t, som holder på b
b = a + b # mens verdiene byttes om
a = t
print(b)Denne koden bruker en brøkdel av et sekund på å beregne F20000, som har 4180 siffer. Så møter python begrensninger i hvor store heltall det liker å regne med uten spesialtilpasninger.
Utvidelser
- Endre funksjonen for å finne trekanttall til også å skrive ut en trekant. Du kan legge til noen print(…) før eller etter funksjonen kalles igjen. Eksempel under for T3:
#
##
###- Kan du få den utskrevne trekanten til å ikke ha en rett kant til venstre, men være sentrert?
- Om du bruker den første, enkle funksjonen for å beregne Fibonacci-tallene, hvor mange ganger kalles funksjonen for å beregne F7? Hva med F10? Kan du finne en rekursiv sammenheng mellom n og antallet funksjonskall?
- Utforsk om differansen mellom to trekanttall kan bli lik en toerpotens 2k?