Programmering gir nye muligheter for å drive utforskende matematikk, spesielt for å teste mange alternativ og gjøre lange beregninger. Noe av det viktigste for å drive utforsking er å stille spørsmål om det du skal utforske. I Walter Browns «The Art of Problem Posing» blir det gitt mange eksempler på aktuelle spørsmål, og hvordan det å identifisere og endre betingelsene kan gi interessante problemer. Målet er å finne problemer som er innenfor rekkevidde for elevene og samtidig utfordrer de.
Det første problemet under krever litt prøving og feiling, og et resonnement om hvorfor \(n^2\) ikke vil ta igjen \(n^3\). Så endrer jeg litt på noen av betingelsene, og vanskelighetsgraden endrer seg. Til slutt kommer en variant som er en skikkelig utfordring i vgs, og som fører frem til \(10^{m-1}(\sqrt{10}-\sqrt[3]{10} + 10\sqrt[3]{10} – \sqrt[3]{100} + 10\sqrt[3]{100} – 10\sqrt{10}) \)
Hvor mange positive heltall \(n\) har like
mange siffer i \(n^2\) som i \(n^3\)?
Dette problemet kan løses på mange måter, det enkleste er nok å prøve seg frem for små tall.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| \(n^2\) | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
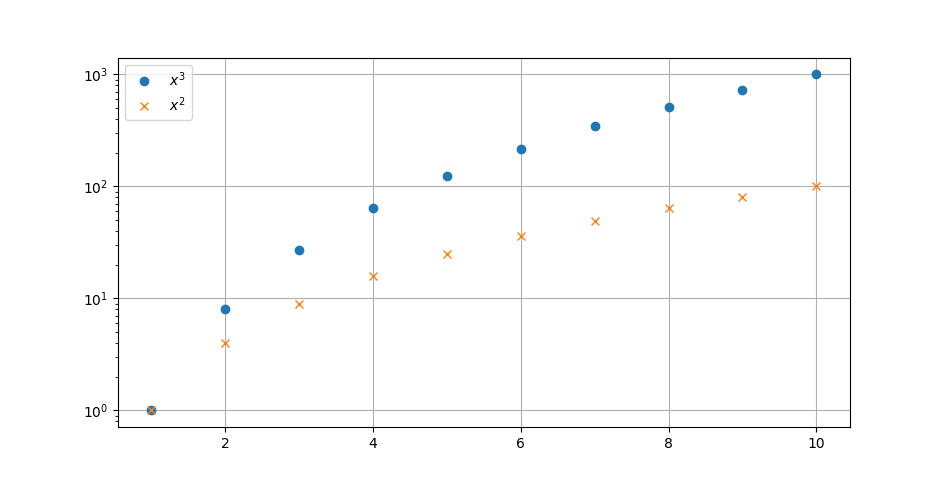
Det ser ut til å gjelde for noen få av disse tallene, for \(n=1\) , \(n=2\) og \(n=4\). Så vokser \(n^3\) raskt, og når \(n^2\) har blitt tresifret, har \(n^3\) allerede blitt firesifret.
Kan du bevise at \(n^2\) aldri igjen får like mange siffer som \(n^3\)?
Utvidelser
Når du har løst et problem, er et godt utgangspunkt for videre utforsking å endre betingelsene. Det kan gjøre problemet både mer vanskelig eller enklere, kanskje helt trivielt eller så godt som umulig. Men det vil uansett lære deg mer om problemet. Kanskje må du også legge inn andre betingelser for å få et godt problem.
Hvor mange positive heltall \(n\) har like mange siffer i \(n^2\) som i \(n^3\)?
Denne er grei. Det vil bli omtrent dobbelt så mange, siden alle negative tall også gir samme antall siffer. I tillegg kommer \(n=0\).
Hvor mange positive heltall \(n\) har like mange siffer i \(n^2\) som i \(n^3\)?
Her trengs det flere betingelser. Hva vil gjelde som et «siffer»? Har \(1{,}5^2 = 2{,}250\) og \(1{,}5^3 = 3{,}375\) like mange «siffer»? Finnes det desimaltall som oppfyller dette når siste siffer etter komma ikke kan være 0? Hvordan vil vi tenke om «siffer» om tallet representeres som brøk?
Hvor mange positive heltall \(n\) har like mange siffer i \(n\) som i \(n^2\)?
Fra tabellen over ser det ut å bare være 1, 2 og 3. Stemmer det? Hva om du bruker andre eksponenter?
Hvor mange positive heltall \(n\) har like mange et færre siffer i \(n^2\) enn i \(n^3\)?
Nå kan du finne mange treff i tabellen over, og det er ikke like opplagt at det vil slutte noen gang. Programmering kan raskt lage en tabell, eller telle antallet treff. Den enkleste måten å telle eller behandle enkeltsiffer i python er å konvertere tallet til en tekststreng først.
Et program som finner slike treff kan være:
opptil = 100 # Hvor langt opp du leter
treff = 0 # Antallet treff til nå
for n in range(1, opptil+1):
# Antallet siffer i n**2 og n**3
s2 = len(str(n**2))
s3 = len(str(n**3))
if s3 - s2 == 1:
treff += 1
print(treff)Hvor mange positive heltall \(n\) har 100 færre siffer i \(n^2\) enn i \(n^3\)?
Her er det best å lete etter et generelt mønster for \(m\) færre siffer. Endre for eksempel programmet over til å lete etter større differanser enn 1, og undersøk opp til høyere verdier. Kan du finne et generelt mønster?
Hint:
Beregnede verdier for noen \(m\), «konvergerer» antallet treff mot en bestemt verdi?
| Antall færre siffer \(m\) | 0 | 1 | 2 | 3 | 4 |
| Antall treff | 3 | 33 | 327 | 3270 | 32704 |
Kan du endre programmet slik at det skriver ut for hvilke \(n\) antallet siffer endrer seg?